Carl Ernst Naumann, in his Über die verschiedenen Bestimmungen der Tonverhältnissen (Leipzig, Breitkopf und Härtel, 1858, p. 19), proposes a representation of the Tonnetz that appears to be the first in Germany after those of Euler and of Weber. It illustrates just intonation, with a notation which is not entirely explicit, similar to that of Oettingen described below. In addition, Roman numerals appear to indicate intervals (with respect to I), gr.III for instance meaning “major third,” IV# meaning “augmented fourth”, etc. The figure (below) extends to distant enharmonies.
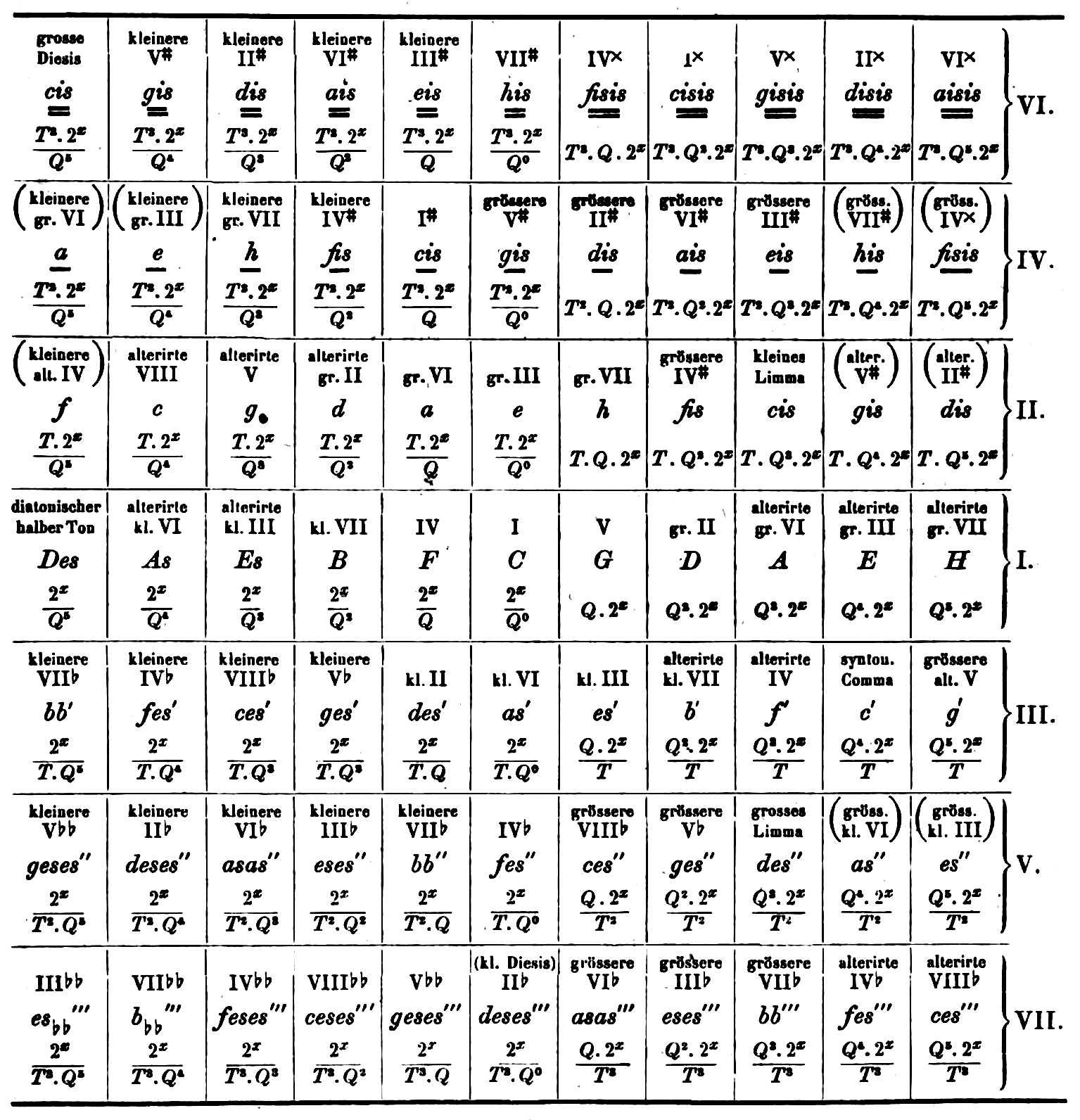
In his Harmoniesystem in dualer Entwickelung (Dorpat, Lepzig, W. Gläser, 1866, pp. 12-16), Arthur von Oettingen discusses just intonation. He first describes his special notation, explaining that because he is not concerned with absolute pitch levels, he will not make use of what is known today as Helmholtz’ notation, but will rather use a notation inspired by Naumann and by Hauptmann, lower case letters throughout, with one or two lines above or under denoting the number of syntonic commas by which they diverge from Pythogarean tuning. The figure below extends to several enharmonies but not as far as in Naumann.
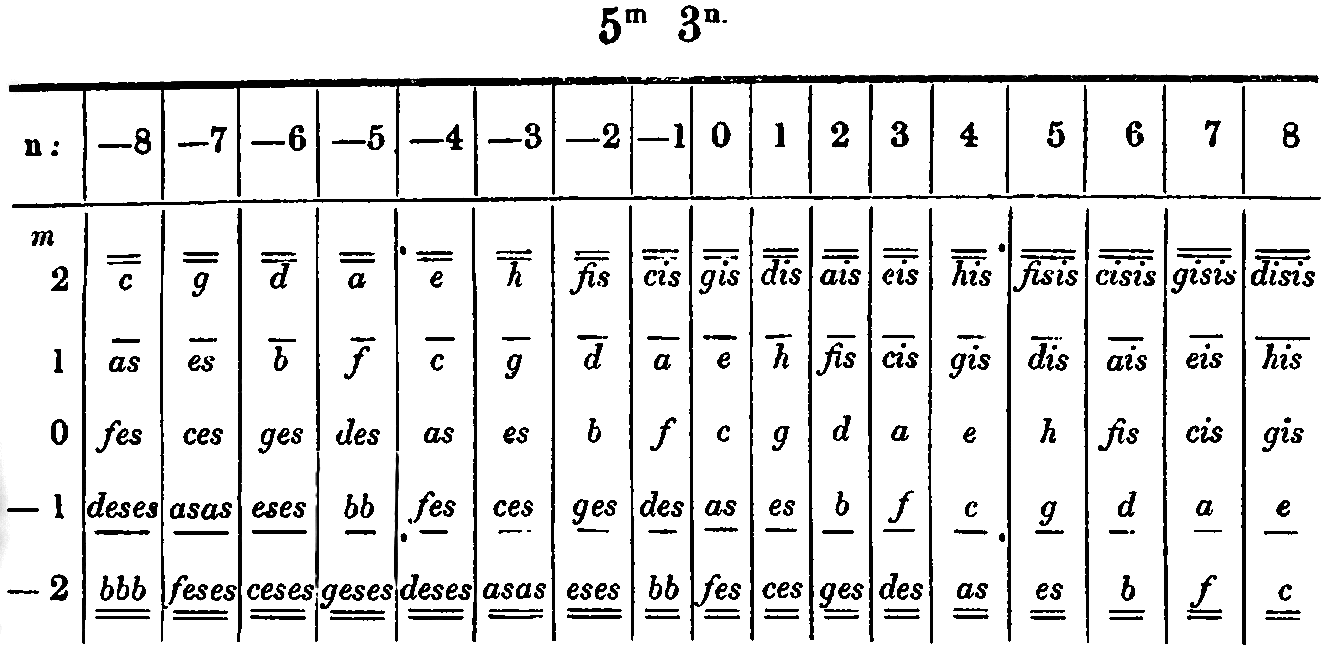
Hugo Riemann, in his Grosse Kompositionslehre (Band I, Der Homophone Satz. Melodielehre und Harmonielehre, Berlin & Stuttgart, W. Spemann, 1902, pp. 478-480), first proposes a similar figure, extending differently both on the horizontal and the vertical axes. He writes (p. 478) that “because there is in our musical system no other type of relation than the fifth- or the third-relation, the table is in fact generally orienting.” He adds (p. 480) that “one could obviously extend the table on all four sides, if one wanted to include more fifths and more thirds”. He explains that the lines above or below each letter show the degree of third-relation (Terzverwandtschaft), e.g. gis [g![]() ] is a degree that, from c (positioned in the middle, denoted by a thicker print), is found by two ascending third progressions (Terzschritte). If one wanted to progress from this c in the horizontal series until reaching a gis, one would need eight fifth progressions to the right. Riemann’s network (p. 478) is as follows:
] is a degree that, from c (positioned in the middle, denoted by a thicker print), is found by two ascending third progressions (Terzschritte). If one wanted to progress from this c in the horizontal series until reaching a gis, one would need eight fifth progressions to the right. Riemann’s network (p. 478) is as follows:
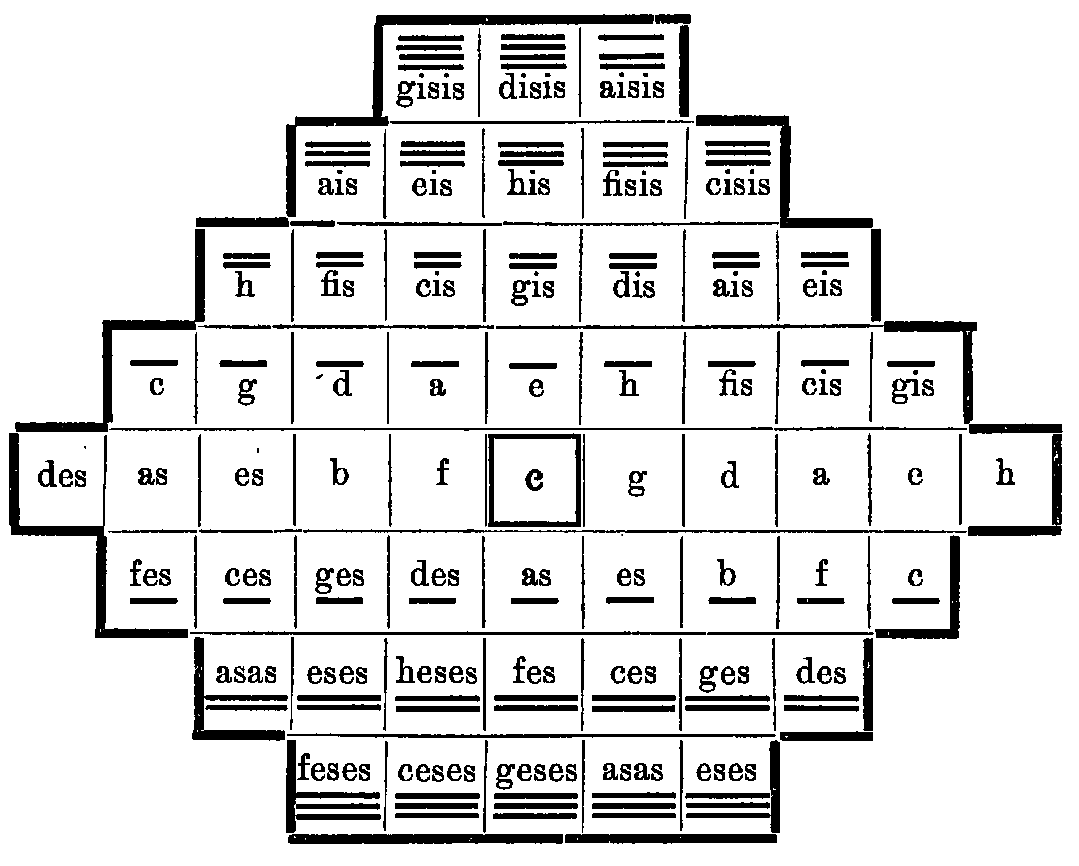
Riemann goes on discussing (pp. 479-480) the usage of this network:
“The degrees of the C major scale and of the A minor scale are found here close together in a tight space:
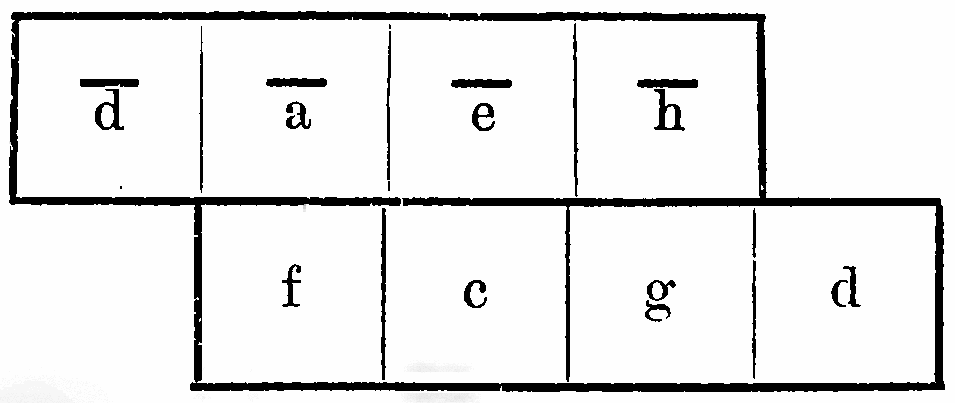
“Each major chord [triad] shows itself in the form of a square bracket open at the top right corner, each minor chord as one open at the bottom left corner:
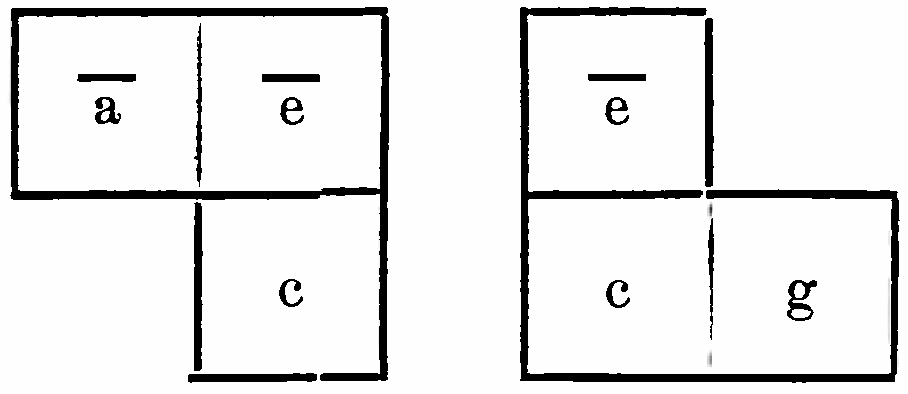
“The fundamentals [Haupttöne] of the three major chords or of the three minor chords in which sense some transposition of the fundamental scale [Grundskala] can be recognized are always positioned in the same horizontal line, for instance:
![]()
[What Riemann apparently means here is that the fundamentals of three triads forming a diatonic scale align in the same way as those of the C major and A minor scales above, which can also be read as formed of three minor chords, d–a–f, a–e–c and e–b–g, or three major ones, a–f–c, e–c–g and b–g–d, each in the form of a square bracket as above. He gives as examples E![]() major (with the three triads on A
major (with the three triads on A![]() , E
, E![]() and B
and B![]() , and C
, and C![]() minor, with the triads C
minor, with the triads C![]() , G
, G![]() and D
and D![]() , in different positions on the Tonnetz, marking the fundamentals with his conventional signs, + for the major and ° for the minor ones.]
, in different positions on the Tonnetz, marking the fundamentals with his conventional signs, + for the major and ° for the minor ones.]
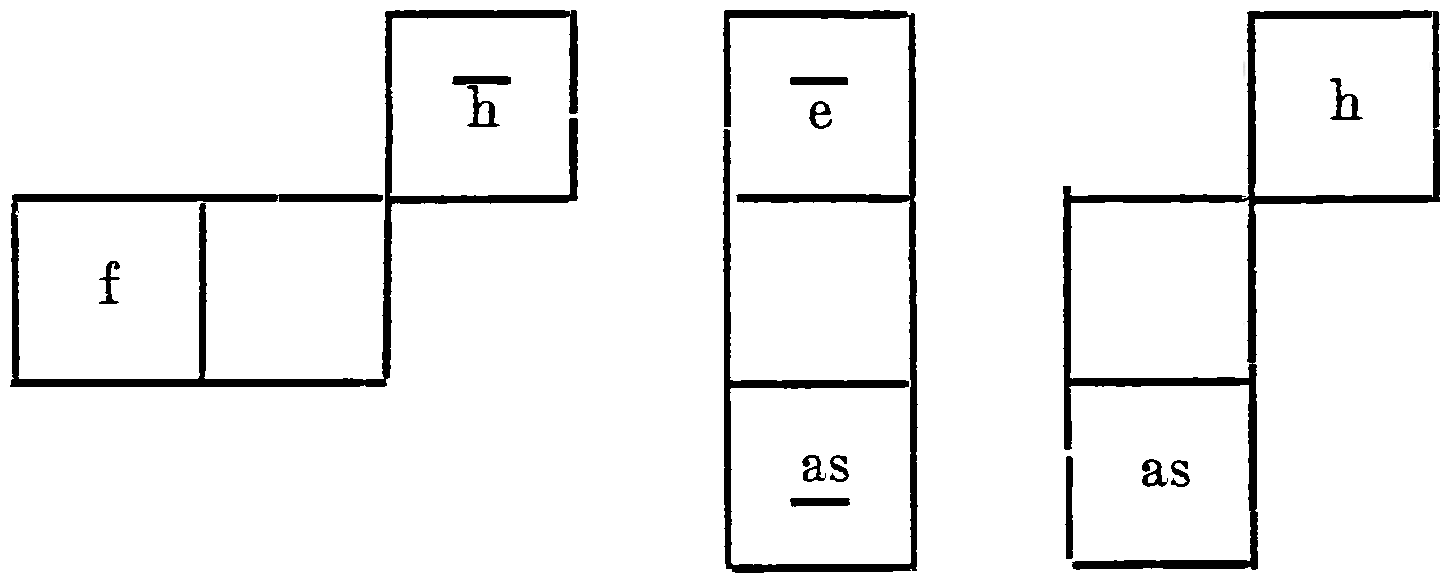
“One will easily determine all other intervals to be considered in music from their simplest derivation in this table, e.g. the augmented fourth [f–b], the augmented fifth [a![]() –e] and the augmented second
–e] and the augmented second
[a![]() –b] as this:
–b] as this:
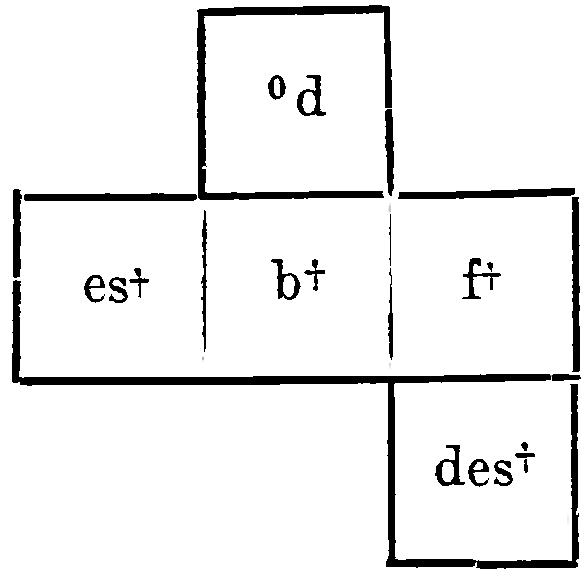
“The keys of G minor, F major, E flat major, D flat major, F major, which the development of Beethoven’s Quartet in B flat major touches, are naturally to be found in the closest proximity to B flat major, with b![]() itself to be imagined as the most convenient center of the tonal system:
itself to be imagined as the most convenient center of the tonal system:
“One cannot determine a defined limit of how far the modulation could distance itself from the principal key, but it is clear that for instance D flat major and F sharp major are too far from each other to enter in direct relation to each other, while G flat major, enharmonically identical with F sharp major, is most closely related to it. ” [Etc.]
It is Riemann’s figure of the Tonnetz, and its mention by David Lewin in Generalized Musical Intervals and Transformations (Yale University Press, 1987, p. 22, footnote), that appears to be at the origin of the American neo-Riemannian theory. Lewin writes that such maps “have been especially common in German theories of tonality since the eighteenth century, generally in connection with key relationships rather than root relationships (though some theories do not dwell on such a distinction).”
There seems however to be no other representation of the Tonnetz after Euler than that of Weber (which is a representation of key relationships) and those of Naumann, von Oettingen and Riemann mentioned above. Schoenberg took them over, in a modified version (his “charts of the regions”), in Structural Functions of Harmony, 1954, 21969, pp. 20 and 30.
N. Meeùs
